第八章 勞動市場
- 工資的意義與種類
- 工資的意義
- 工資
勞動者提供勞務,在一段時間之內的報酬
工資=工資率*總工作時數 - 工資率
指勞動的提供者在單位時間之內的報酬 - 工資的種類
- 計時工資
按照工作時間的長短來計算工資,如速食店 - 計件工資
按照所完成的工作件數來計算工資 - 貨幣工資
勞動者在每一單位時間之內,提供勞務所得到的貨幣報酬 - 實質工資
勞動者所賺得貨幣工資的購買力,亦即,實質工資為貨幣工資除以物價水準的結果
實質工資↑,購買力↑,物質生活水準↑ - 勞動的需求
廠商對勞動的需求是一種引申的需求,因為廠商雇用勞動的目的,不在勞動本身,而是藉由勞動去生產最終財貨 - 廠商的生產決定
廠商利潤最大時,其產量決定於MR=MC,雇用工人時,也是相似的考量 - 從邊際產量到邊際收益產量
- 兩個假設:
- 假設廠商的產品在完全競爭市場出售,也就是假設廠商是價格的接受者
- 假設廠商將工資視為固定,亦即廠商雇用工人數較少,所以無法影響工資
- 邊際產量(MP)
每增加一位勞動雇用量時,總產量的增加量 - 邊際產量遞減
在其他條件不變之下,隨著勞動雇用量的增加,總產量的增加量呈現遞減的現象 - 邊際收益產量(MRP)
每多雇用一位勞工時,總收益的增加量 - 勞動的邊際收益產量等於工資(MRP=W)
追求最大利潤的廠商,會雇用勞工在工資與邊際收益場量相等之處,即MRP=W
因為: - 當W>MRP時,表示廠商付給勞工的工資,大於勞工對廠商的貢獻,所以追求最大利潤的廠商,會減少對勞工的雇用
- 當W<MRP時,表示廠商付給勞工的工資,小於勞工對廠商的貢獻,所以追求最大利潤的廠商,會增加對勞工的雇用
- 綜合上述兩者,廠商雇用工人的標準為MRP=W
- 廠商的引申需求與市場需求
- 勞動的供給
- 出外工作、家庭工作與休閒
- 工資變動的影響:所得效果與替代效果
- 所得效果
當工資提高時,人們選擇工作時數較少,而不是較多工作時數 - 替代效果
因為工資提高而使得我們工作更多的時間 - 勞動供給曲線的型態

- A圖,替代效果大於所得效果
- B圖,替代效果等於所得效果
- C圖,替代效果小於所得效果
- 後彎的勞動供給曲線

- 工作與取得人力資本
工人生產力的高低,取決於教育年限的多寡與在職訓練的有無 - 勞動市場均衡

- 工資差異的原因
- 生產力的不同
勞動的邊際生產力高,工資就高 - 特殊才藝
當某項才藝,供給彈性小,以及需求高時,會帶動工資的價格 - 人力資本的投資
人力資本的取得與累積與有形資本的取得一樣,都需要投入時間與金錢 - 種族與性別的原因
種族與性別歧視,使得同工不同酬 - 工作的風險
與工作相關的風險越高,工資也越高 - 補償性工資差異
具有同質的工人,因為工作地點、工作時間、工作性質的不同,也會產生工資的差異 - 工會與勞工
- 工會的功能與作法
工會的成立,其目的在於勞工工資率的提高與勞工福利的保障,其目的與廠商希望低工資率,呈現取捨關係。
- 直接要求高於均衡的工資率
要求高工資,使得部分勞工失業 - 工會減少勞動的供給
減少供給,提高工資
方法有: - 提高入會費限制一些有意加入的會員
- 以證照制度限制會員資格
- 在短期之內減少會員的工作時數,逼迫資方讓步
- 工會設法增加勞動需要
增加勞動需要,來提供工資
- 限制進口
透過限制進口,促使供給減少,來造成國產車價格上漲,進而擴大勞動需要 - 限制工會會員的工作時數
工作時數受到限制,自然得多聘員工來增產 - 支持限制外勞政策
減少外勞數量,促使廠商增加對本國勞工的需要 - 提高生產力
- 強迫雇用
例如,防止廠商引用機械科技,來避免員工的流失 - 外籍勞工問題
- 移民經濟學的基本理論
- 波哈斯認為移民的影響
- 正面
低工資、低技術的新移民使得勞動市場更具競爭,廠商可以較低的薪資雇到勞工而獲利,消費者也可以購買到廉價的物品 - 負面
移民多數經濟情況較差,長期依賴社會福利的結果,成為美國財政上的負擔。
另外,也搶走多數當地勞工的工作機會。 - 總結:兩個效果
- 移民使得整個社會的總產出增加
- 移民會造成所得重分配的結果
- 波哈斯認為解決失業問題的方法為,當經濟景氣好、失業率低時,提高移民人數;當經濟景氣差、失業率高時,降低移民人數。
--------------------------------
- Consider the following game, called matching pennies, which you are playing with a friend. Each of you has a penny hidden in your hand, facing either heads up or tails up (you know which way the one in your hand is facing). On the count of “three,” you simultaneously show your pennies to each other. If the face-up side of your coin matches the face-up side of your friend’s coin, you get to keep the two pennies. If the faces do not match, your friend gets to keep the pennies.
- Who are the players in this game? What are each player’s strategies? Construct a payoff matrix for the game.
A:
The payoff matrix should look like the one below:
- Is there a dominant strategy? If so, what?
A:
No, neither player has a dominant strategy. Recall that a dominant strategy is one that yields a higher payoff regardless of the strategy chosen by the other player. In this game, if your friend chooses Heads, then your payoff is higher when you choose Heads. On the other hand, if your friend chooses Tails, then your payoff is higher when you choose Tails. Since your best course of action varies depending on what your friend does, you do not have a dominant strategy. Similarly, if you choose Heads, then your friend is better off choosing Tails, and if you choose Tails, then your friend is better off choosing Heads. Thus, your friend also does not have a dominant strategy - Is there an equilibrium? If so, what?
A:
No, there is no equilibrium. As discussed in part b, you will always be better off when you chose the same side as your friend; however, if both sides match, then your friend will be better off choosing a different side, but if your friend changes sides, then you too will want to change sides - In studying for his economics final, Sam is concerned about only two things: his grade and the amount of time he spends studying. A good grade will give him a benefit of 20; an average grade, a benefit of 5; and a poor grade, a benefit of 0. By studying a lot, Sam will incur a cost of 10; by studying a little, a cost of 6. Moreover, if Sam studies a lot and all other students study a little, he will get a good grade and they will get poor ones. But if they study a lot and he studies a little, they will get good grades and he will get a poor one. Finally, if he and all other students study the same amount of time, everyone will get average grades. Other students share Sam’s preferences regarding grades and study time.
- Model this situation as a two-person prisoner’s dilemma in which the strategies are to study a little and to study a lot, and the players are Sam and all other students. Include the payoffs in the matrix.
A:
The strategies, players and payoffs are shown in the following payoff matrix:
Benefits:
Good grade: 20
Average grade: 5
Poor grade: 0
Costs:
Study a lot: 10
Study a little: 6
the upper-left corner and the lower-right corner, Sam and the other students are doing the same thing (either all studying a lot – upper-left or all studying a little – lower-right). In this case they will all receive an average grade and a benefit of 5. The costs of studying a lot are 10 so the payoffs in the upper-left corner are a benefit of 5 less a cost of 10 or ‘-5’. The costs of studying a little are 6 so the payoffs in the lower-right corner are a benefit of 5 minus a cost of 6 or ‘-1’.
In the lower-left, Sam studies a little and all other students study a lot. For Sam, the benefits with the poor grade are ‘0’ with costs of 6 and a payoff of ‘-6’. For the other students who are studying a lot, the benefit of a good grade are 20 less the cost of studying a lot of 10 resulting in a payoff of ‘10’.The outcomes in the upper-right are just the opposite. Sam studies a lot, gets a good grade with a payoff of ‘10’. Other students study a little, get a poor grade with a payoff of ‘-6’ - What is the equilibrium outcome in this game? From the students’ perspective, is it the best outcome?
A:
The equilibrium outcome for this game is for Sam and the other students to study a lot and receive an average grade. Both the other students and Sam would be better off if everyone studying a little because it would have led to the same grade, but at a lower cost - Blackadder and Baldrick are rational, self-interested criminals imprisoned in separate cells in a
dark medieval dungeon. They face the prisoner’s dilemma displayed in the matrix.

Assume that Blackadder is willing to pay $1,000 for each year by which he can reduce his sentence below 20 years. A corrupt jailer tells Blackadder that before he decides whether to confess or deny the crime, she can tell him Baldrick’s decision. How much is this information worth to Blackadder?
A:
The information is worth nothing to Blackadder since he knows that both he and Baldrick have the same dominant strategy, which is to confess - Newfoundland’s fishing industry has recently declined sharply due to overfishing, even though fishing companies were supposedly bound by a quota agreement. If all fishermen had abided by the agreement, yields could have been maintained at high levels.
- Model this situation as a prisoner’s dilemma in which the players are Company A and Company B and the strategies are to keep the quota and break the quota. Include appropriate payoffs in the matrix. Explain why overfishing is inevitable in the absence of effective enforcement of the quota agreement.
A:
The strategies, players and payoffs are shown in the following payoff matrix:
Starting in the upper-left cell, if both companies keep the quota, then fish stocks are large, and each company regrets not having broken the quota, because they could have earned higher profits by doing so. In the lower-right cell, both companies break the quota, and neither regrets it, because keeping the quota while the other company breaks it would lead to low profits. In the off-diagonal cells, one company earns higher profits from overfishing (which it does not regret), but the other suffers lower profits. Each company’s dominant strategy is thus to break the quota, which means that both will do so unless some way can be found to enforce the quota - Provide another environmental example of a prisoner’s dilemma.
A:
If Firm A pollutes from its factory and no one else does, then it gains from not
having to install pollution-control equipment (which leads to lower costs and higher profits), as well as from clean air, since my own pollution has only a negligible effect on air quality. However, if all other industrialists think this way, the air will become polluted, and all firms will be worse off than if none had polluted. Profits may also be lower if all firms pollute because the cost advantage of polluting will be shared by all firms, and competitive forces (entry) will reduce prices and profits. - In many potential prisoner’s dilemmas, a way out of the dilemma for a would-be cooperator is to make reliable character judgments about the trustworthiness of potential partners. Explain why this solution is not available in many situations involving degradation of the environment.
A:
In many potential prisoner’s dilemmas, a way out of the dilemma for a would-be cooperator is to make reliable character judgments about the trustworthiness of potential partners, but in situations involving environmental degradation, the players usually do not know each other and there is thus no opportunity to make character judgments. In such cases, legal enforcement is often necessary - Two airplane manufacturers are considering the production of a new product, a 150 passenger
jet. Both are deciding whether to enter the market and produce the new planes. The payoff
matrix is as follows (payoff values are in millions of dollars).

The implication of these payoffs is that the market demand is large enough to support only one manufacturer. If both firms enter, both will sustain a loss. - Identify two possible equilibrium outcomes in this game.
A:
The two possible equilibrium outcomes are:
i. Boeing produces and Airbus does not;
ii. Airbus produces and Boeing does not.If the manufacturers find themselves in one of these two cells, neither will want to change its strategy. For example, consider the case in which Boeing produces and Airbus does not. Given that Airbus does not produce, if Boeing changes its strategy to "Don't Produce", its payoff will fall from $100 million to $0. Similarly, given that Boeing produces, if Airbus changes its strategy to "Produce", its payoff will fall from $0 to -$5 million. Thus, each company is making the best choice given the other company's choice. A similar argument can be made about the case in which Airbus produces and Boeing does not - Consider the effect of a subsidy. Suppose the European Union decides to subsidize the
European producer, Airbus, with a check for $25 million if it enters the market. Revise the payoff
matrix to account for this subsidy.What is the new equilibrium outcome and why?
A:
Revised payoff matrix that includes subsidy to Airbus:
Because of the subsidy, producing is now a dominant strategy for Airbus. And, since Boeing knows that Airbus will produce, it will choose not to produce - Compare the two outcomes (pre- and post-subsidy). What effect does the subsidy have?
A:
In the absence of the subsidy, neither Boeing nor Airbus has a dominant strategy, and there are two possible equilibrium outcomes. One in which Boeing is the only manufacturer, and the other in which Airbus is the only manufacturer. The subsidy changes the game because it makes entering the market a dominant strategy for Airbus. Knowing this, Boeing will not enter the market, and Airbus will be the sole manufacturer. - Jill and Jack both have two pails that can be used to carry water down from a hill. Each makes only one trip down the hill, and each pail of water can be sold for $5. Carrying the pails of water down requires considerable effort. Both Jill and Jack would be willing to pay $2 each to avoid carrying one pail down the hill, and an additional $3 to avoid carrying a second pail down the hill.
- Given market prices, how many pails of water will each child fetch from the top of the hill?
A:
In this situation, each player’s payoffs are independent of the action taken by the other. Each pail of water sells for $5, and since the cost of carrying each pail is less than $5, Jack and Jill will each carry 2 pails of water - Jill and Jack’s parents are worried that the two children don’t cooperate enough with one another. Suppose they make Jill and Jack share equally their revenues from selling the water. Given that both are self-interested, construct the payoff matrix for the decisions Jill and Jack face regarding the number of pails of water each should carry.
What is the equilibrium outcome?
A:
When the two children are forced to share revenues, their payoff matrix is as follows:
This game is a prisoners’ dilemma. The dominant strategy for both Jill and Jack is to carry only one pail down the hill, even though each would be better off if both carried two pails. Therefore, their parents’ plan creates an equilibrium with total payoffs of $6 rather than $10! - The owner of a thriving business wants to open a new office in a distant city. If he can hire someone who will manage the new office honestly, he can afford to pay that person a weekly salary of $2,000 ($1,000 more than the manager would be able to earn elsewhere) and still earn an economic profit of $800. The owner’s concern is that he will not be able to monitor the manager’s behaviour and that the manager would therefore be in a position to embezzle money from the business. The owner knows that if the remote office is managed dishonestly, the manager can earn $3,100, while causing the owner an economic loss of $600 per week.
- If the owner believes that all managers are narrowly self-interested income maximizers, will he open the new office?
A:
The owner knows that if he opens the remote office (top branch at A), the potential manager’s best strategy is to be dishonest (bottom branch at B), in which case the owner earns a loss of $600. Since the owner loses money by opening the remote office, he will decide against opening the new office. - Suppose the owner knows that a managerial candidate is a devoutly religious person who condemns dishonest behavior, and who would be willing to pay up to $15,000 to avoid the guilt she would feel if she were dishonest.Will the owner open the remote office?
A:
In this case, the owner knows that if he opens the remote office, the potential manager’s best strategy is to be honest since $3,100 - $15,000 = -$11,900. Thus, the owner will open the remote office - Consider the following “dating game,” which has two players, A and B, and two strategies, to buy a movie ticket or a baseball ticket. The payoffs, given in points, are as shown in the matrix below. Note that the highest payoffs occur when both A and B attend the same event.
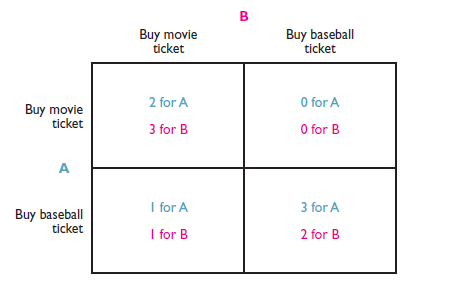
Assume that players A and B buy their tickets separately and simultaneously. Each must decide what to do knowing the available choices and payoffs but not what the other has actually chosen. Each player believes the other to be rational and self-interested. - Does either player have a dominant strategy?
A:
No, neither player has a dominant strategy since the best choice for each player depends on what the other player does - How many potential equilibria are there?
(Hint: To see whether a givencombination of strategies is an equilibrium, ask whether either player could get a higher payoff by changing his or her strategy.)
A:
The top-left and bottom-right cells are both potential equilibria, since in each of these cells neither player has any incentive to change strategies. - Is this game a prisoner’s dilemma? Explain.
A:
No, the payoffs in this game do not follow the pattern associated with a prisoner’s dilemma because neither player has a dominant strategy - Suppose player A gets to buy his or her ticket first. Player B does not observe A’s choice but knows that A chose first. Player A knows that player B knows he or she chose first. What is the equilibrium outcome?
A:
Player A knows that if he or she has the first move and buys a movie ticket, so will player B, in which case player A will get a payoff of 2. If player A buys a baseball ticket, so will player B, in which case player A will get a payoff of 3. Player A will therefore buy a baseball ticket, and so will player B - Suppose the situation is similar to part d, except that player B chooses first. What is the equilibrium outcome?
A:
The reasoning is the same as for part d, except this time both players will see a movie - Consider the following game. Harry has four quarters. He can offer Sally from one to four of them. If she accepts his offer, she keeps the quarters Harry offered her and Harry keeps the others. If Sally declines Harry’s offer, they both get nothing ($0). They play the game only once, and each cares only about the amount of money he or she ends up with.
- Who are the players? What are each player’s strategies? Construct a decision tree for this game.
A:
The decision tree should look like the one below:
- Given their goal, what is the optimal choice for each player?
At point B on the decision tree, Sally’s payoff will be higher if she accepts, no matter what K is. So her best choice is to accept. Knowing this, Harry gets the highest payoff by choosing K = 1. Sally’s payoff will be $0.25, and Harry’s will be $0.75 - Imagine yourself sitting in your car in a campus parking lot that is currently full, waiting for someone to pull out so that you can park your car. Somebody pulls out, but at the same moment a driver who has just arrived overtakes you in an obvious attempt to park in the vacated spot before you can. Suppose this driver would be willing to pay up to $10 to park in that spot and up to $30 to avoid getting into an argument with you. (That is, the benefit of parking is $10 and the cost of an argument is $30.) At the same time he guesses, accurately, that you too would be willing to pay up to $30 to avoid a confrontation and up to $10 to park in the vacant spot.
- Model this situation as a two-stage decision tree in which his bid to take the space is the opening move and your strategies are (1) to protest and (2) not to protest. If you protest (initiate an argument), the rules of the game specify that he has to let you take the space. Show the payoffs at the end of each branch of the tree.
A:
Decision tree for this problem:
- What is the equilibrium outcome?
A:
Since your payoff is -$30 if you protest and $0 of you defer, it is in your best interest to defer. Anticipating this, the other driver will steal your spot since his payoff is $10 of he steals your spot and $0 if he leaves the spot for you. So, the equilibrium outcome is $0 for you and $10 for the other driver - What would be the advantage of being able to communicate credibly to the other driver that your failure to protest would be a significant psychological cost to you?
A:
Suppose the other driver believed that you would experience a psychological cost of $30, not only if you got into a dispute, but also if you failed to protest his unjust behavior. In that case, your payoff when deferring would be -$30, making this the worst outcome for you. The other driver would then know that attempting to steal the spot at A would make you protest at B, thereby giving him a payoff of -$30. Therefore, the other driver would be better off leaving the spot for you, and the equilibrium outcome would be $10 for you and $0 for the other driver.

沒有留言:
張貼留言